Note
4.8(9)
Chat with Kai
AP Calculus BC Study Guides
AP Calculus BC Ultimate Guide
Unit 1: Limits and Continuity
Unit 2: Differentiation: Definition and Fundamental Properties
Unit 3: Differentiation: Composite, Implicit, and Inverse Functions
Unit 4: Contextual Applications of Differentiation
Unit 5: Analytical Applications of Differentiation
Unit 6: Integration and Accumulation of Change
Unit 7: Differential Equations
Unit 8: Applications of Integration
Unit 9: Parametric Equations, Polar Coordinates, and Vector-Valued Functions
Unit 10: Infinite Sequences and Series
Studying for another AP Exam?
Check out our other AP study guides
Unit 1: Limits and Continuity
Limits
- Limits are the value that a function approaches as the variable within the function gets nearer to a particular value.
- We don’t really care what’s happening at the point, we care about what’s happening around the point
- To find the limit of a simple polynomial, plug in the number that the variable is approaching
Ways to Find Limits
Look on a graph to see what it approaches
- If the graph approaches two different values for the same number, the limit does not exist
Estimate from a table
Algebraic Properties
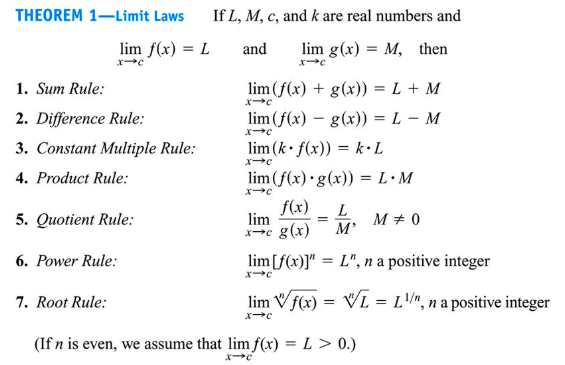
Algebraic Manipulation
- You can factor the numerator and denominator, then cancel any removable discontinuities
- This is mostly useful if you get limits where the denominator is equal to 0
For example, (x+3)(x+2)/(x+3)(x-3)
- (x+3) is able to be removed → removable discontinuity
Squeeze Theorem
- Conditions
- For all values of x in the interval that contains a, g(x) ≤ f(x) ≤ h(x)
- g and h have the same limit as x approaches a
- lim g(x) = L, lim h(x) = L, therefore lim f(x) = L
- Trig limits as x approaches 0:
- lim [sin(x)/x] = 1
- lim [(cos(x)-1)/x] = 0
- lim [sin(ax)/x] = a
- lim [sin(ax)/sin(bx)] = a/b
Continuity
- Jump Discontinuity
- Occurs when the curve “breaks” at a particular place and starts somewhere else
- The limits from the left and the right will both exist, but they will not match
- Essential/Infinite Discontinuity
- The curve has a vertical asymptote
- Removable Discontinuity
- An otherwise continuous curve has a hole in it
- “Removable” because one can remove the discontinuity by filling the hole
- Continuity Conditions
- For f(x) to be continuous when x=c:
- f(c) exists
- the limit as x→c exists
- lim f(x) = f(c)
- x→c
- A function is continuous on an interval if it is continuous at every point on that interval
Removing Discontinuities
- You can remove a discontinuity by redefining the function without that point in the domain
- This is frequently done by factoring out a common root between the numerator and denominator
Limits and Asymptotes
- Vertical asymptote: a line that a function cannot cross because the function is undefined there
- Horizontal asymptote: the end behavior of a function
- A horizontal asymptote can be crossed
Horizontal Asymptote Rules
- If the highest power of x in a rational expression is in the numerator, then the limit as x approaches infinity is infinity: there is no horizontal asymptote
- If the highest power of x is in the denominator, then the limit as x approaches infinity is zero and the horizontal asymptote is the line y=0
- If the highest power is the same, then the limit is the coefficient of the highest term in the numerator divided by the coefficient of the highest term in the denominator
Intermediate Value Theorem
- Guarantees that if a function f(x) is continuous on the interval [a,b] and C is any number between f(a) and f(b), ten there is at least one number in the interval [a,b] such that f(x) = C
Note
4.8(9)
Chat with Kai
AP Calculus BC Study Guides
AP Calculus BC Ultimate Guide
Unit 1: Limits and Continuity
Unit 2: Differentiation: Definition and Fundamental Properties
Unit 3: Differentiation: Composite, Implicit, and Inverse Functions
Unit 4: Contextual Applications of Differentiation
Unit 5: Analytical Applications of Differentiation
Unit 6: Integration and Accumulation of Change
Unit 7: Differential Equations
Unit 8: Applications of Integration
Unit 9: Parametric Equations, Polar Coordinates, and Vector-Valued Functions
Unit 10: Infinite Sequences and Series
Studying for another AP Exam?
Check out our other AP study guides